x and y intercepts

For those of you who watch or play football, then you are familiar with the term 'interception.' For those of you who aren't, well, stop and think for just a second what interception just might mean…

Why all this talk about football? Isn't this a website about math? Yeah, sure but let's take a look at football for a second and then make the connection to math, shall we?

In a linear equation, y = mx + b,

a point where the line crosses the y-axis
it is the number when x is zero (0)
is represented by the letter b in the linear equation y = mx + b

In football, a quarterback (offensive player) for team A throws a pass. Unfortunately, a defensive player from team B intercepts the ball before someone from team A can catch it.

Team B is thrilled! They have thwarted the other team! Bummer for Team A…

So, how does all of this relate to math and linear equations?

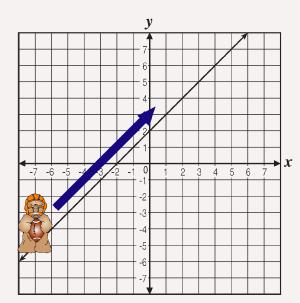
Pretend that the quarterback is throwing the ball and the path it is taking is the line.

Here is a picture to help you 'get' it. We always read from left-to-right so the quarterback is on the left. He throws the ball to the right so the ball is going UP. Let's see what happens.

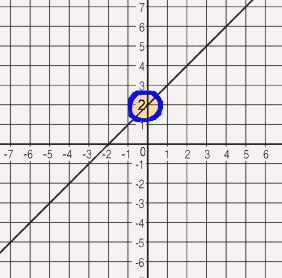
Team B (the y-axis) intercepts the pass. In this picture, the point of interception is circled.

This means that the point where the line crosses the y-axis is the point of interception or the y-intercept.

The point the line crossed is at (0, 2).

In the linear equation formula, y = mx + b, think of the b as ball.

In a coordinate pair your numbers are set up (x, y). If we are looking for the 'y' for our ball for the y-intercept, which one would it be from our point? Did you say 2? Hooray!

Just substitute THAT number in the equation!

y = mx + 2

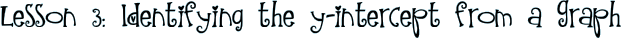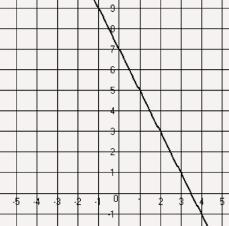
Cool! Now that you understand the vocabulary from a football point-of-view and you know the definition of what a y-intercept is, let's see how you can find the y-intercept from looking at a graph.

Step 1: Look at the line. Find where it crosses the y-axis.

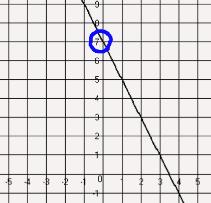
Step 2: Draw a CIRCLE around the point where the line crosses the y-axis.

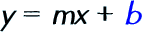Step 3: Write down the basic linear equation form y = mx + b.

Substitute the number you circled for the b.

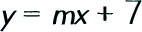Step 4: Go find the slope to finish your equation! y = mx + b.

So, after all this y-intercept talk, what about the x-intercept? Huh?

Here's the deal…you have been working with the x-intercept but just didn't know it. The x-intercept is the point where the line crosses the x-axis. (Duh!) Think about it…the y-intercept is the point where a line crosses the y-axis, right? So, doesn't it make sense that the x-intercept is the point where the line crosses the x-axis? See? It isn't anything new.

The BIG question now isn't going to be finding it on the graph but how do you find it if you have an EQUATION like this:

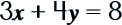How do you find both the y- and x-intercept in an equation like this?

This isn't as hard as it may seem. Check it out.

Step 1: Substitute ZERO for each variable.

To find the x-intercept, substitute the y with a 0.

To find the y-intercept, substitute the x with a 0.

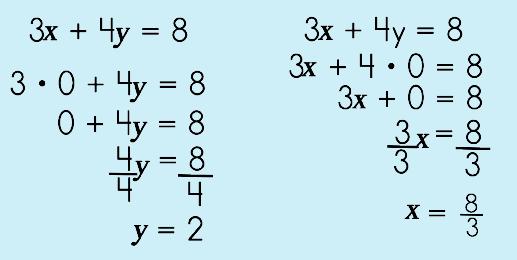Step 2: Solve for the variable in the equation.

The equation on the left side gives you the y-intercept!

The equation on the right side gives you the x-intercept!

That's it! Voila!

Easy-peasy, lemon-squeasy!