Functions vs. Relations

	You need to be aware of the terminology when learning about functions and relations. This stuff comes up all the time on tests and if you understand the terminology, it is half the battle. (As Mrs. S-S always says, knowing the vocabulary will help you pass the test!)

relation: a set of ordered pairs; think of it as a relationship between sets of information

the domain is the set of all first numbers of the ordered pair (x, y), later on we will learn this as the Independent Variable

the range is the set of all second numbers of the ordered pair (x, y), later on we will learn this as the Dependent Variable

function: a very special type of relation where each domain has its very own range value or each x has its very own y value (each x has one y value). In other words, each input x has its own output y partner.

Let's see what this LOOKS like.

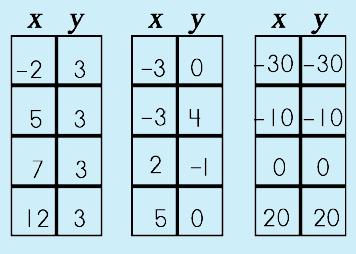
	Just from looking at these three examples, it is somewhat difficult to tell which group(s) may or may not be a function. One way to make it a bit easier is to organize it in a table form.


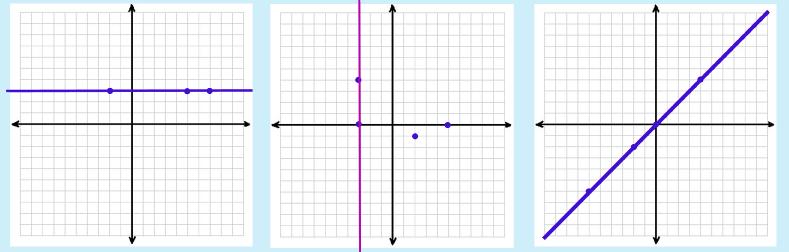
	So, let's do that and see if it helps. A-ha~! Yes, this DOES make it easier! Example 1~ each x has the same y. This is a function, an unusual function, but a function nonetheless (it does follow our rule, right?). *One way to think about it is this: You CAN'T share the domain (x)! The range value can be the same as long as the domain value isn't. The Vertical Line Test will prove why…* Example 2~ two of the y have the same x so this is NOT a function. Example 3~ each x has its own y. So, this is the only group that is a function See what happens with the Vertical Line Test is this: IF you have two or more y values that share an x, then you will be able to draw a vertical line through the points (duh…get it? "Vertical Line"). Here are the three graphs that go with the relations.

	You can see the vertical pinkish-colored line in the second graph…a result of the two points (-3, 0) and (-3,4).

Well, one way to test for functions is the method we just LOOKED at in the three examples above! That wasn't too hard, right?

There are others (of course!).

If you can fit your x and y values in the form y = … where you have a unique y, then, hey, you've got a function!

There is a special 'test' called the Vertical Line Test that can also help determine if a relation is a function or not. This one is a no-brainer because all you have to do is one thing: check that each x has a unique y partner. In other words, just by looking at the domains (x) you can tell right away! If you find that there are two of the same number, then BINGO. The relation is NOT a function.

Here is a typical math problem.

Use the vertical-line test to determine whether each relation is a function.




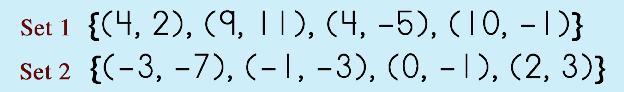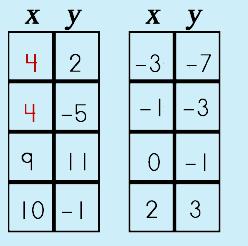	Step 1: Check domain (x) Look to see if you have two or more of the SAME domain (x value). *Putting them into a table form is easiest for me but plotting the points makes an easy visual

	Step 2: Check for unique range (y) partners Check to see that the x and y have unique partners. Remember that y is dependent on x and in order to be a function, each x must be paired with a different y. That's it!

So, in these two cases, we can say that Set 1 is NOT a function because there are two points, (4, 2) and (4, -5), that share the same domain and this is a no-no.

Set 2 follows the rule and each x and y have unique partners and fits the Vertical Line Test making it a function.