Scientific notation…you may remember learning about this back in pre-algebra but it promptly left your This is why it is included here as a review to jog your memory because it is used in algebra!

Scientific notation is the way to write really big numbers as well as really small numbers using exponents. It is oftentimes used by scientists and found in scientific measurements, , hence the term, 'scientific notation.'

Using scientific notation is simple because all need to do is count decimal places! You simply take a number and re-write it as a base number times ten raised to a power.

Let's review how it works.

Step 1: Move the decimal so it comes after the FIRST digit (number). This number is called the mantissa.

Step 2: Count the number of decimal places you moved the decimal.

Step 3: Write the exponent as a power of 10 with the number you counted.

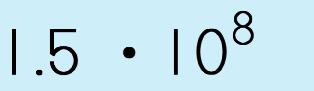Step 4: Write out the expression as mantissa • 10 ^power

Rules? Yes, there are ALWAYS rules to follow but these rules make sense so stop complaining.

1. If your exponent is NEGATIVE, then your number is small. Think about it. 3.543 • 10^-4. What direction are you going?
2. If your exponent is POSITIVE, then your number is LARGE.
3. A number without an exponent has a number 1 for its exponent.
4. A power tells you how many times the number is MULTIPLIED by 10. (duh!)
5. If you move the decimal point to the LEFT to create the scientific notation, the power of 10 is positive. For example, 315 = 3.15 • 10²
6. If you move the decimal point to the RIGHT to create the scientific notation, the power of 10 is negative. For example, 0.023 = 2.3 • 10^-2

©2011–2017 Sherry Skipper Spurgeon.

All Rights Reserved.