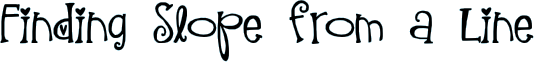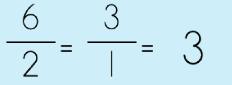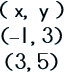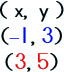How to Find Slope





Slope is one of those concepts in pre-algebra that seem SO difficult to learn but, when broken down into several short lessons, can be VERY easy! Yep, its' true! (trust me, I know what I'm talking about here) The important thing to remember is that you really have to pay attention and follow some simple rules because otherwise, well, you'll just be falling right off of the mountaintop and that is NO fun!

First things first: What IS slope?

Slope is:

the steepness of a line
comes in four types: positive, negative, zero, and undefined
is a ratio and never changes
represented by the letter m in the linear equation y = mx + b (this is also called the slope-intercept form)

As much as you probably are tired of hearing about the 'F' word, well, you are going to hear about it again right here. AND, you are going to LOVE it. Yeah, yeah, yeah…you're thinking, "Sure, Mrs. S-S." Ha! You will soon be saying, "Fractions are my BFF!" once you learn how they will help you with slope! Check it out… (and, forget about the book and that phrase 'rise over run' which always got ME confused because I could never remember which way to start—just stick with your BFF!)

Step 1: Take a look at your line.

Heavily mark two points (shown here in red).

You are going to draw a right triangle from the two points.

*I like to use the y-intercept as one of the points but you don't have to.

The hypotenuse of the triangle is your line.

Step 2: Drop a line down from one point and over from the other point to make a right triangle.

Step 3: Count the height of your right triangle.

Write this as your numerator.

In this example, the little curves indicate that the height of this right triangle is six (6) squares. So, the numerator is 6.

*If you learned the 'rise over run' method, then this is the rise number.

$fraction1$

Step 4: Count the base of your right triangle.

Write this as your denominator.

The little curves indicate that the base of this right triangle is two (2) squares. So, the denominator is 2.

*For those of you recording this as rise over run, this is the run number.

$fraction2$

$fractiontofraction$

Step 5: Reduce your fraction to lowest terms (if possible).

You have come up with the slope.

That's it…easy-peasy, lemon-squeasy!

IF you are substituting it into the linear form y = mx + b, then simply substitute it as y = 3x + b.

IF you knew that the y-intercept was -2, THEN, the entire equation for the line would be: y = 3x – 2

Being able to identify the shape of the slope line is often half the battle, especially if you are given one of those multiple-choice tests where you aren't sure how to figure out the slope (because you forgot about drawing the triangle and your BFF!!). So, look at these pictures because you just might be able to answer those test questions by the skin of your teeth…

REMEMBER: Slope is always determined from LEFT to right.

One way to help you with the 'positive vs. negative is to draw a stick figure! Keeping in mind that when you READ, you READ from left-to-right so remember that when you read slope you also read it from left-to-right.

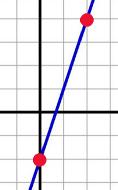
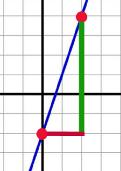
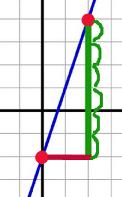
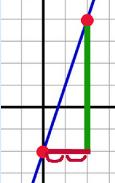
Sometimes you know two coordinate pairs (the name of the points) and need to find the slope. ARGH! What to do? It's all arithmetic, my dear! Check it out…

Let's say these are your points:

Step 1: Re-arrange the points.

Write your points so that they line up vertically like this.

Step 2: Color-code each pair (with two points, you need two colors).

Remember: coordinate pairs are written (x, y)

Step 3: Re-write the numbers using the point-slope formula. Since everything is color-coded, this is really easy. Just substitute the numbers…

Step 4: Do the math. That's it!

You now have found the slope.

The slope is:



Why is it that some math books give homework assignments where an equation is NOT in the correct form and we have to put it into the 'correct form?" This is enough to drive a kid crazy! Slope-intercept is one of those cases that pops up all the time in algebra. So just how do you do it?


	Here's an equation:	What you need to do is put it into the form y = mx + b so let's follow the steps…


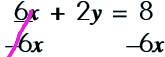	Step 1: Use inverse operations to move terms on the y side over to the OTHER side.

	Step 2: Finish solving the equation for y. Divide the coefficient in front of the y by both sides of the equation.

	Step 3: Check to be sure the equation is in the correct form: y = mx + b If necessary, re-arrange the terms (good ol' commutative property!). That's it!

				becomes

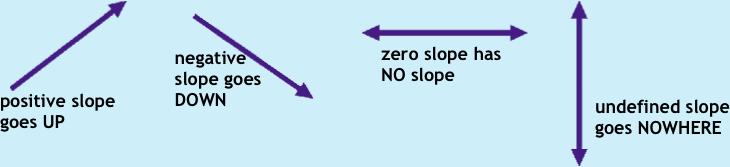
And you thought you knew all there was to know about slope! Ha!

Direct variation is an unchanging, constant ratio that goes with the mathematical statement, "y varies directly as x." Huh? In plain English, this means that when x changes, y changes by the same ratio. Whew!

Now, it can be expressed by a formula (of course!) in two ways, with k as the constant.



		or

Since k is the constant and is always the same, never changing for each point, you can find it quite easily. It is a simple division problem! Yep, that's right! Think about it for a second…

What would you have to do if you had the following problem (comes from an Algebra book)?


	*Is this equation a direct variation? If it is, find the constant of variation.*

	Step 1: Put the equation into your slope-intercept form Step 2: Look at the slope! That's it. Easy-peasy, lemon-squeasy!



		Yes, this is a direct variation. Constant is 7.5 (slope is 7.5)

Another way to look at the direct variation… To calculate the constant of variation, just find the slope!