 |
||||
 |
||||
In pre-algebra, we began using exponents with terms but predominantly did the four basic operations (adding, subtracting, multiplying, and dividing). Being able to use these four operations with ease is an expectation in Algebra. If you are having some difficulty, then please refer back to the Pre-algebra Bugs Me section on Exponents. We are moving forward now so get ready!
Quick Review |
||
|
|
||||||||||||||||
|
|||||||||||||||||
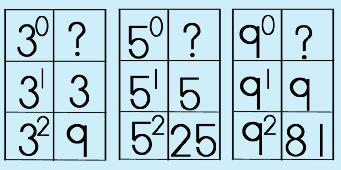
One of the first properties that you need to understand is the Zero Property of Exponents. This one is pretty basic. It actually is a fundamental one that sort of makes sense, in a way IF you make a table of some numbers…so, let's take a look and see what happens. |
||
So, what do you think? What might the value of a number be when you raise it to the power of zero? Hmmm…Think about this one for a bit…It will actually make sense if you really concentrate! Did you come up with 1 (one)? Hooray! That's right! Any number (or term, for that matter) when raised to the power of zero will have a value of 1. It wouldn't be zero (0) because if you were to go in reverse (inverse), then you would realize that that you could NOT divide by zero because your quotient is undefined. |
||||
 |
||||
We can look at it from my favorite…a fraction (tee-hee!). So, let's see what I mean by that, shall we? Here we have two exponents written as a quotient (fraction). If we simplify it, what do we get? A-ha! |
||||
 |
||||
 |
||||
EEEK! It's either the word 'negative' or the word 'fraction' that always freaks people out in math. Goodness gracious! Take a chill pill! This is really SO easy! You are going to be shocked when you see just how simple negative exponents really are…trust me on this one. (Of course, you are going to have to NOT be lazy here either so this may take some work on YOUR part!). Okay, so if you are ready… |
||
We have this number with a negative exponent. Now, before we go ANY further, just think for a second about what we have learned about that negative sign…what do you know about it? What does it MEAN? Okay, keep that in the back of your mind. |
||||
Hmm…Did you think to youself something like, "That negative sign means to take the OPPOSITE and when you are using exponents you are multiplying so I should take the OPPOSITE or the multiplicative inverse of the base so I should DIVIDE." If you did, then you are on the right track! Let's see how this works. |
||
Re-write the base in its inverse form. Then, write the exponent with the base. That's it! |
||||||||
What if you have negative exponents mixed in within a term? How do you simplify THAT?
|
||
 |
||||
Start by circling the term that contains the negative exponent. |
||||
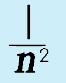 |
||||
Re-write the negative exponent. |
||||
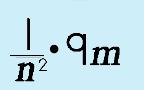 |
||||
Now, multiply the two terms… |
||||
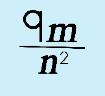 |
||||
That's it! |
||||
 |
||
©2011–2017 Sherry Skipper Spurgeon. All Rights Reserved. |
||