When you have a fraction like

, you already learned this is a rational number, right? Well, if you take an expression

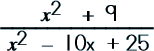like

or

or

then you have what is called a rational expression.

Now, because you already know about rational number rules, you can transfer some of that to rational expressions! Yep, that's right!

Denominators: For example, can you have a zero in the denominator of a rational number? Nope. So, you cannot have a zero in the denominator of a rational expression either! Or, in algebra we would say that you 'exclude zero from the domain.' (Doesn't that sound so much more sophisticated anyway?)

Lowest-Terms or Simplest Form; When writing rational numbers (or, if you are thinking of them as 'fractions') you always want your number in lowest terms or simplest form, right? The same thing occurs with rational expressions. Your rational expression is in simplest form when the numerator and denominator have no common factors except 1. Let's continue, shall we?

A common problem that comes up in algebra would be something like this…

Simplify each of the following rational expressions.

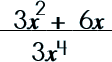Step 1: Factor the numerator.

Find the Greatest Common Factor and factor out the numerator, if possible.

 

Note that the third rational expression's numerator remains as is.

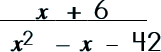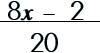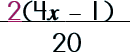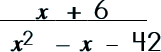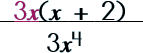Step 2: Factor the denominator.

Do the same with the denominator, if possible.

 

In the first two rational expressions, there was nothing to factor but you could factor the the third expression.

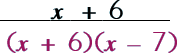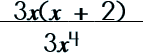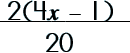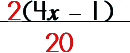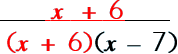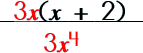Step 3: Reduce/cancel by dividing.

That's it!

Easy-peasy, lemon-squeasy!

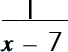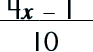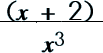Okay, now that you see that working with rational expressions is just like working with good ol' fractions, well, can you just imagine what multiplying and dividing with them is going to be like? Hmmm…not too difficult to guess what the answer is going to be, right? The same thing! Woo-hoo!

=

Now, before you get too excited and start multiplying and dividing those rational expressions on your homework, let's pause a moment here and think about what we should do BEFORE jumping right in to do those computations. Back when you worked with fractions, what did you do before you did your multiplying/dividing? Do you remember? Okay, hotshot. Did you say, "Find the Greatest Common Factor or Divisor," or something like that? If you did, then you ARE a hotshot! If not, well, then you probably were getting a little too excited about math! tee-hee! Let's take a look at the best way (I think!) to go about multiplying and dividing rational expressions.

Step 1: Look to see what can be factored.

Does either numerator need factoring?

Does either denominator need factoring?

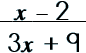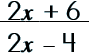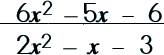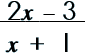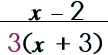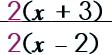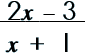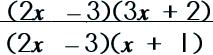Step 2: Divide out the common factors.

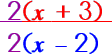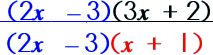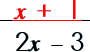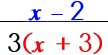Step 3: Simplify what's left.

That's it! Easy-peasy, lemon-squeasy!

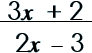©2011–2017 Sherry Skipper Spurgeon.

All Rights Reserved.