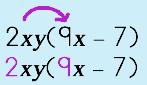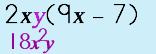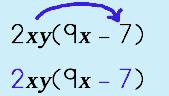 |
||
Multiplying polynomials is a very basic operation in algebra. In fact, it is something you've been doing for a very long time and probably never realized you were doing it! We'll take it one step at a time so that you can make the connection from your past experiences and see just how sensible it is. (I know, you're thinking, "Sensible? Since when is algebra sensible? Trust me…in this case, it REALLY is!" Since vocabulary is part of this, we'll go nice and slow. |
||
 |
||||
|
||||||||||||||||
Simplify: |
||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Step 1: Use the Distributive Property. Distribute the TERM across the parenthesis to the FIRST term.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Step 2: Distribute the TERM across the parenthesis to the SECOND term.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||
If you can multiply a monomial with a binomial, then you can multiply two binomials because the process is the same. You will be using the Distributive Property again. Follow along! |
||
Simplify: |
||||||||
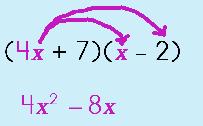 |
||||||||
Step 1: Use the Distributive Property. Distribute the FIRST TERM across the second binomial.
|
||||||||
Step 2: Distribute the SECOND TERM across the second binomial.
|
||||
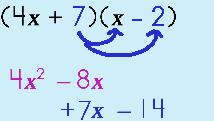 |
||||
Step 3: Simplify.
|
||||||||||
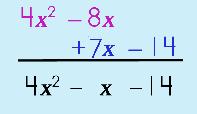 |
||||||||||
 |
||||||||||
Easy-peasy, lemon-squeasy! |
||||||||||
Ahhh…sometimes there are those math problems that LOOK easy and then you find you had the wrong answer. You wonder to yourself, "What did I do wrong?" Let's take a look at what happens when you have a binomial that is raised to the second power. |
||
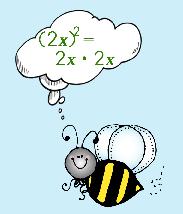 |
|||||||||
Simplify: |
|||||||||
First, THINK…GEMA (Order of Operations) What does that exponent tell you to do? In GEMA you do what is within the grouping symbols first (can't do anything yet), then exponents, right? SO, what would you do if you saw a term raised to an exponent? A-ha! |
|||||||||
You can now simplify like you normally do using the Distributive Property OR you can use the method below. Why would do that? Well, because there's a cool PATTERN that goes with squaring binomials. It is so awesome that you are going to LOVE it! Check it out… |
||
Original problem |
||||
Step 1: Square the first term.
|
||||
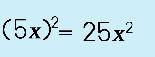 |
||||
Step 2: Square the second term.
|
||||
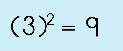 |
||||
Step 3: Multiply the two terms. Now, double the product.
|
||||
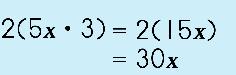 |
||||
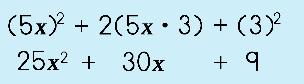 |
||||||||||
Step 4: Put them together and you're done!
|
||||||||||
 |
||||||||||
Easy-peasy, lemon-squeasy! |
||||||||||
Chill! You already know what to do so relax! If you stopped to think it through, you have all the skills to do these types of 'hard' problems (they really aren't that hard either…). Okay, let's take a peek at one. |
||
Simplify: |
||||
|
|||||||||
Since you already have a method for solving squared binomials, you can use it to your advantage. Let's use it for this problem. |
||
Original problem: |
||||
Step 1: Square the binomial.
|
||||
|
||||
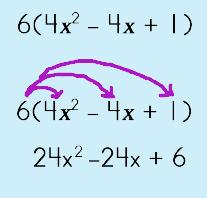 |
||||||||||
Step 2: Use the Distributive Property to multiply the resulting trinomial with the monomial.
|
||||||||||
 |
||||||||||
Easy-peasy, lemon-squeasy! |
||||||||||
You can also utilize the 'box method' aka 'generic rectangles' to multiply polynomials. Check out the page that shows you how to do this! Just click here. |
||
©2011–2017 Sherry Skipper Spurgeon. All Rights Reserved. |
||