What the heck is an inequality? Hmm…look at the word. There's a word within that you do know, and in fact, you DO know this CONCEPT because you learned it way back in elementary school.

Do you remember these 'Pacman' or 'sharkmouth' or 'alligator' symbols? < and > or ≤ and ≥

Well, these symbols represent inequalities! Inequality means something that is not equal. Makes sense, right? If you simply subsitute the inequality symbol for the equals sign, then, voila! Your equation can be solved just like any old equation. Easy-peasy, lemon-squeasy!

NOW, there's just one teensy-weensy little difference; the way you show your solution set (aka, answer). You won't be getting a single answer here in one of these types of equations so you need ways to show these answers. Here ya go!

Let's say you have something like this: x < 4

What are some of the possible values you could have for x? 2, 3, 1, -7, …

The answers are infinite! The answers to an inequality are called the solution set.

An easy way to show the answer is to graph the solution set as a number line.

If you start plotting the points that fit the solution, you would get something that begins to look like…Can you see the line beginning to form?

Now, the only thing is, the x is less than 4 but not including 4. So, when you actually draw your line, you would draw an OPEN circle at the 4. This shows your solution does NOT include 4. Your number line would look like:

What if you have something like: x – 5 ≥ -3

First, how would you solve it? Think of the inequality sign as an equals sign (let's just change it to an equals sign for now) so you can see what I mean). Then I bet you can solve it easily.

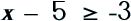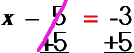Solve for x like you normally would.

Then, at the end, just go back and replace the = with the ≥. Voila!

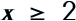Now, to graph your solution set on the number line…Let's see.

First of all, we know that x can = 2. But, x can also be > 2. So, if we start plotting points, the number line would look like:

Since the inequality symbol is ≥ the circle is colored IN when drawing the line.

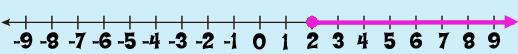Instead of graphing the solution set you can use set notation. You may recall using braces (or curly brackets) back in elementary school; it shows up once again!

Let's refer back to our previous example to show how set notation is used.

Of course, there is still another method to showing the solution set to an inequality…something called interval notation. It's kind of like a cross between the number line and set builder notations (sort of) because if you know the two then this one isn't all that difficult (truly!). Are you ready to learn it? Here we go!

Let's use our previous example, once again. This time we will use BOTH examples because the notations are slightly different for the regular ol' < and > versus the ≤ and ≥.

Now, don't worry if you don't get these interval notations as we won't be doing too many of 'em in class. If you at least have had some experience with 'em then that's pretty good.

Sometimes you will end up with an equation where you are working with a negative variable. With inequalities, there's something rather unique that happens. Let's take a look at an example to see what I mean.

Here's our example…

…and the worked out problem.

Let's try some possible answers to see if our solution set works before we draw a graph.

Possible answers…

5, 6, 7, …

OH NO!

There's a PROBLEM!! -7 is most definitely not greater than -4.

When you are working with inequalities and you have a NEGATIVE variable, guess what you must do to an inequality sign…you have to FLIP IT in order for your solution set to work.

Solution set: