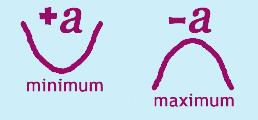There's more than one way to skin a cat. EWWWW! Okay, we aren't skinning cats here but you may have heard that old proverb before…So, there's also more than one way to find the vertex of a quadratic function!

My feeling is always, find the method that best works for Y-O-U! Personally? I think this is a much EASIER way to find the vertex because, a) I can always re-write the equation into this form using all those lovely properties (you know the ones: Associative, Commutative, Distributive…) and b) it seems to be a more VISUAL form and when things are in a visual form, they are obviously easier to SEE. I'm sure lots of folks will disagree but that's okay. You decide.

The 'vertex' form for writing a quadratic function looks like this.

y = a(x-h)² + k, where (h, k) is the vertex

Let's see what this looks like when it applies to some 'real' functions.

Find the vertex of this parabola.

Finding the Vertex

Step 1: Find the vertex of the parabola

By looking at the equation, you can actually identify what the (k, h) will be because it fits the form! This will give you the vertex or axis of symmetry.

Step 2: Determine if the parabola opens up or down (minimum or maximum point)

 

Look at the 'a' coefficient. This will tell you if your parabola is going to open UP (with a minimum point) or DOWN (with a maximum point).

 

In the case of this particular equation, since the a coefficient is +1, our parabola will open UP with a minimum point.

That's it! Easy-peasy, lemon-squeasy!

Are you ready to try a few other functions to see how it works? Come on! We'll even see how to go from the STANDARD form to the Vertex Form…totally awesome.

Here's the problem:

Step 1: Find the Vertex

Look at the parenthesis. This is where we are going to find our x.

Uh oh…there's a negative sign in FRONT of the parenthesis. In fact, it's a -3 so the +2 becomes a -6.

 

The -7 stays the same.

 

So, our vertex is (-6, -7). So far so good…

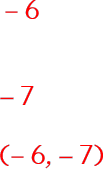Step 2: Determine if the parabola opens up/down and has minimum/maximum vertex

Okay, looking at the original function, there's a -3 sign in front of the parenthesis. This means theh parabola will open DOWN, thus having a MAXIMUM vertex.

 

Whoa! Was that easy or what?

Relax! If the function is not in this Standard form but is in the regular ol' quadratic function equation form (you know the one, y = ax² + bx + c), then you can easily put it INTO Standard Form by doing what's called 'COMPLETING the SQUARE.' Completing the square is a form of factoring, which, of course, we've done a LOT of.

Go on to the Completing the Square now, if you need some help.

©2011–2017 Sherry Skipper Spurgeon.

All Rights Reserved.